I just watched The Dollar Game - Numberphile, in which a game involving graphs is presented. I recommend you watch the video for complete information.
The game involves a graph with integer values on its nodes, positive and negative. For instance, the following graph:
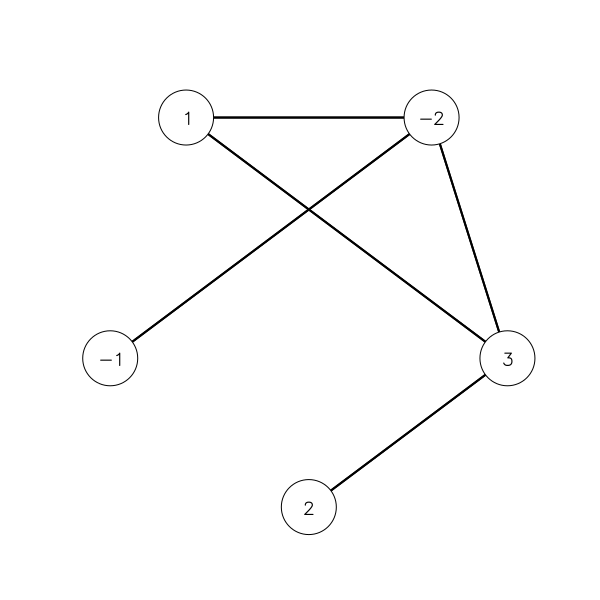
Each node corresponds to a person, the node value is the amount of money that person has, the edges are the people that person can give or take money from. The objective of the game is to have everyone have a non-negative amount of money. In each move of the game, one person decides to give or take money, however, that person either takes 1 dollar from each of their connections, or gives 1 dollar to each one.
On Numberphile, there are two questions: (i) does the problem has a solution? (ii) what’s the least amount of moves to find it? I’ve decided to implement this problem using optimization, since it looked almost straightfoward. The optimization model was indeed very simple, and it took more time drawing graphs than modelling. Still fun though.
The model
Given the undirected graph $G = (V, E)$, and values $w_i, i \in V$, our model is based on the following observations:
- The order of moves is irrelevant;
- Whether the move is a give or a take, is just a question of sign;
- The value of a node after the moves can be computed by accounting for the moves done by the done and by its neighbours.
Hence, we can model it using two non-negative integer variables $g_i$ and $t_i$ storing the number of gives and takes of node $i$. Notice that we could use $y_i = g_i - t_i$, but this is more descriptive.
- Objective: minimize the number of moves
$$\min \sum_i (g_i + t_i)$$
- Constraint: after the moves, the values of the nodes should be non-negative
$$ w_i + \sum_i (t_i - g_i) |N_i| + \sum_{j \in N_i} (g_j - t_j) \geq 0, \qquad \forall i \in V. $$
As it turns out, it’s a very simple model. The implementation is also very simple. We’re using Julia Language with the JuMP modelling language, and the LightGraphs package from JuliaGraphs. Here’s the code:
function dollar_game(g, W)
nv = length(vertices(g))
model = Model(solver = CbcSolver())
@variable(model, give[1:nv] >= 0, Int)
@variable(model, take[1:nv] >= 0, Int)
@objective(model, Min, sum(give[i] + take[i] for i = 1:nv))
@expression(model, x[i=1:nv], W[i] +
(take[i] - give[i]) * length(neighbors(g, i)) +
sum(give[j] - take[j] for j = neighbors(g, i)))
@constraint(model, x .>= 0)
status = solve(model)
println("status = $status")
if status != :Optimal
return zeros(nv), W
end
give = Int.(getvalue(give))
take = Int.(getvalue(take))
sol = Int.(getvalue(x))
println("give = $give")
println("take = $take")
println("sol = $sol")
return give - take, sol
end
The code should be pretty self-explanatory, but ping me on twitter if you need clarification.
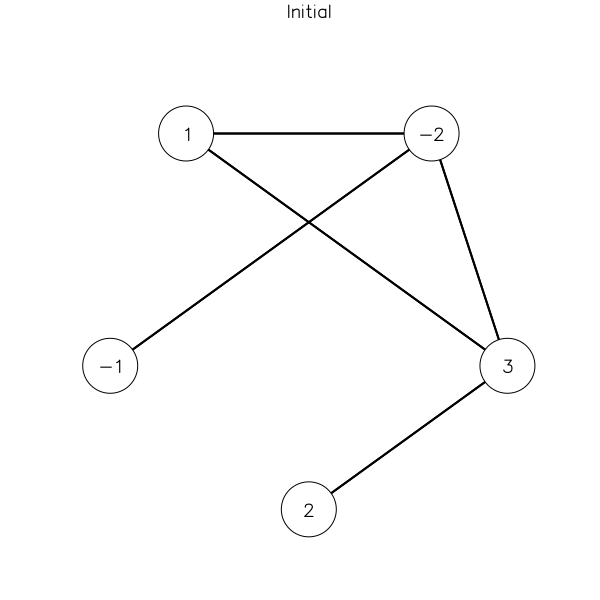
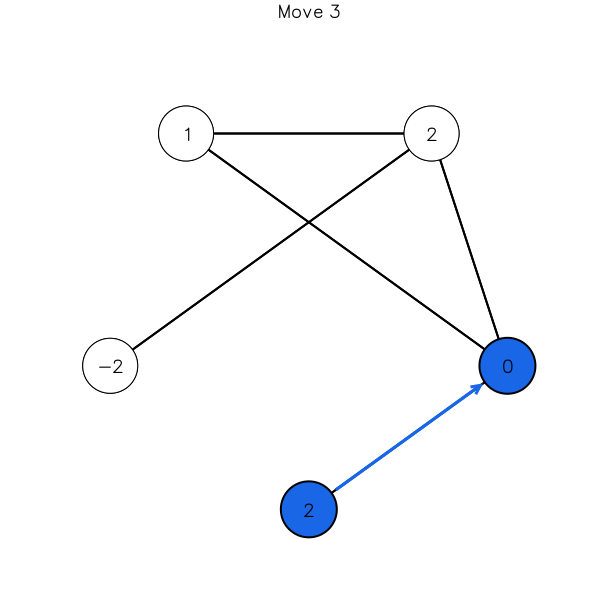
Using the results and mad plotting skillz the packages Plots and GR, we
obtain a solution for the problem above. The moves are illustrated below, where
blue means giving, and red means taking.




The full code is available at GitHub.