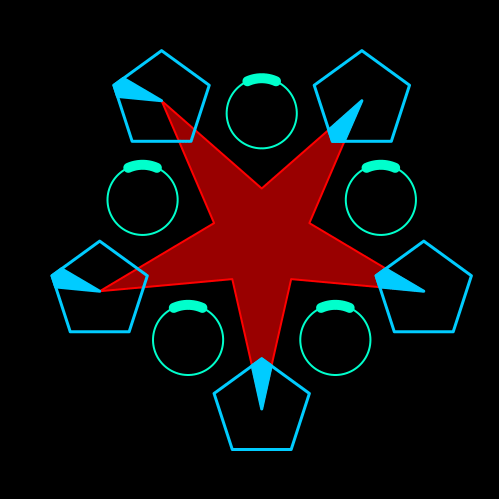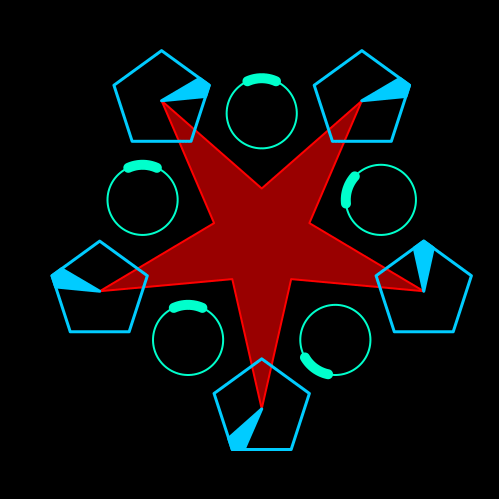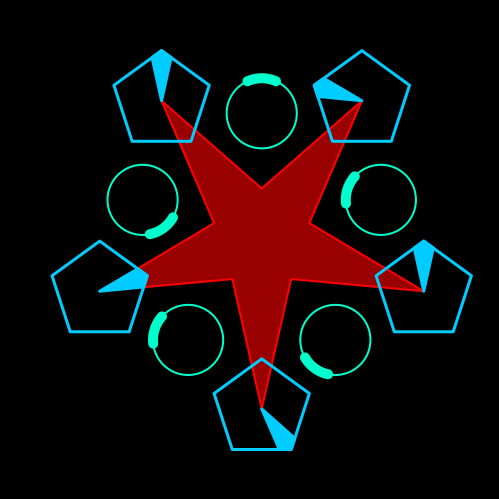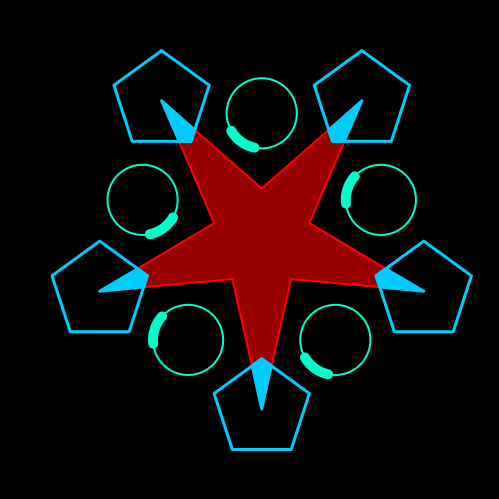
I have a new video out where I talk about solving an RPG puzzle using Julia:
You can check the pluto notebook html here or download the notebook here.
Here’s a more fantastic setup than I used in the video:
You walk into a large room with a 3 pointed star painted on the floor. Three triangular stones sit on top of the points of the star. One of the points of the triangle complement the point of the star, indicating that there is a correct orientation for it. Around the star, 3 circular stone platforms stand with a circular crank in the middle. The crank can be turned clockwise or counter-clockwise, but it only stops at three positions: the initial position, a third of a full rotation, or two thirds of a full rotation. Moving the cranks make the triangles move as well (I will not explain here how, see the gif below or the video). You have to find the configuration that aligns the triangle with the star.
Here’s an animated version of the rotation:
The 3-dial version should be easy enough to solve without slowing down the game. The idea in this game was to activate a teleport. To make it more challenging, when two triangles are aligned, a rift to the astral plane appears and githyanki pirates randomly appear. That being said, if your players really hate puzzle and want to brute force the solution, they might eventually try to force the triangle to turn. What to do?
Forcing the triangles directly
The basic solutions for your players to try to turn the triangles directly are:
- Say “you can’t” (which is not great).
- Say “you do it” (which invalidates the existence of the puzzle).
Instead, we can say “no, but”:
“When you force the triangle (with a DC 20 Str, maybe?), the triangle gives move a little/an inch, but a much stronger force holds it from moving more. However, you can see that the dials also moved a little. When you release the triangle, the dials also move back”.
The idea here is that there is a sequence of movements in the dials that will essentially move only one of the triangle. This goes back to linear algebra working for modular arithmetic (see video). The displacement of the triangles is given by the following equation:
$$ \begin{bmatrix} \Delta t_1 \\ \Delta t_2 \\ \Delta t_3 \end{bmatrix} = \Delta t = A \Delta d = A \begin{bmatrix} \Delta d_1 \\ \Delta d_2 \\ \Delta d_3 \end{bmatrix}. $$
where $\Delta t_i$ is the angular displacement of the triangle $i$, $\Delta d_i$ is the angular displacement of the dial $i$, and $A$ is a matrix. All of these values are modulo 3 for our puzzle. See the video or the notebook for the actual matrix $A$. The relevant conclusion here is
$$ \Delta d = A^{-1} \Delta t,$$
that is, you can see how the dials should move when the triangles are moving. So if you want to move the first triangle clockwise once, you can just look at the first column of $A^{-1}$. If you want to move the second triangle counter-clockwise once, you can just look at the opposite of the second column. If you have enough players, they could push all triangles at the same time, and just the see the solution directly.
Notice that this only works because the set of modulo 3 numbers has 3 values. This means that the movements can be describe as either “stands still”, “moves clockwise”, or “moves counter-clockwise”. For the harder 5-dial version, it is harder to describe in an immersive kind of way. Also, it probably is not a fun in-game puzzle.
But if you want to try to solve the 5-dial version, here is the animation showing the dial movements:
And if you want to see the animated solution, look here:
Solution