I just released a video about using mathematical modeling to solve a production planning with the thematic of selling your art on the beach.
You can check the pluto notebook html here or download the notebook here.
I have an excert down here, but for more details, check the video.
In Brazil, a common joke between undergrad students (usually during exams) is that “maybe I should give up and go sell my art on the beach”.
In this series, let’s follow a situation like that, by following the story of Javier, who just decided to leave his applied math program and sell beaded jewelry.
Javier spends his days on the beach, where he showcases his products, and while not selling, he can work on more of them. It’s a simple life.
However, while working on his art, Javier’s mind wanders into his optimization class. He realizes that he could some use some of the basics of that class to improve his production.
Javier has 3 products:
- Necklaces
- Bracelets
- Earrings
To create these products, he uses 3 materials:
- Beads
- String
- Wire
Let’s simplify, and assume all necklaces are equal, all bracelets are equal, etc.
For each product, you have a different use of materials, a different selling price, and a different time to assemble them. Additionally, there are costs for the materials. Finally, Javier assumes that having variety is good for business, so he wants at least some amount of each product. These values can be seen in the video.
Modeling
The way that Javier learned to model was using the Sets, Parameters, and Variables.
Sets:
- Products: $p \in \mathcal{P}$
- Materials: $m \in \mathcal{M}$
Parameters:
| Name | Unit | Identifier | Set |
|---|---|---|---|
| Time availability | h | $\text{time_available}$ | |
| Product $p$ selling price | € / unit | $\text{selling_price}_p$ | $p \in \mathcal{P}$ |
| Material $m$ cost | € / [$m$] | $\text{material_cost}_m$ | $m \in \mathcal{M}$ |
| Hours to assemble product $p$ | h / unit | $\text{assemble_time}_p$ | $p \in \mathcal{P}$ |
| Minimum production of product $p$ | unit | $\text{min_prod}_p$ | $p \in \mathcal{P}$ |
| Amount of $m$ per unit of $p$ | [$m$] / unit | $\text{mat_per_prod}_{p,m}$ | $p \in \mathcal{P}, m \in \mathcal{M}$ |
Variables:
- Amount of product $p$ assembled and sold (unit): $\text{prod}_p, \quad p \in \mathcal{P}$
Expressions:
Revenue: $$\text{revenue} = \sum_{p \in \mathcal{P}} \text{selling_price}_p \times \text{prod}_p$$
Total Used Material: $$\text{total_used_material}_m = \sum_{p \in \mathcal{P}} \text{mat_per_prod}_{p,m} \times \text{prod}_p, \quad m \in \mathcal{M}$$
Total Material Cost: $$\text{total_material_cost} = \sum_{m \in \mathcal{M}} \text{total_used_mat}_m \times \text{material_cost}_m, \quad m \in \mathcal{M}$$
Time expenditure: $$\text{time_spent} = \sum_{p \in \mathcal{P}} \text{assemble_time}_p \times \text{prod}_p$$
Objective:
- Maximize profit: $$\text{maximize} \quad \text{revenue} - \text{total_material_cost}$$
Constraints:
- Time Availability: $$\text{spent_time} \leq \text{time_available}$$
- Minimum production: $$\text{prod}_p \geq \text{min_prod}_p, \quad p \in \mathcal{P}$$
- Integer production: $$\text{prod}_p \in \mathbb{Z}$$
Code
The code below needs data to work, so check the video or the code (links in the top).
using JuMP, Cbc
function optimize_production(time_availability)
model = Model(Cbc.Optimizer)
set_attribute(model, "logLevel", 0)
products_index = Dict(p => i for (i, p) in enumerate(products))
materials_index = Dict(m => i for (i, m) in enumerate(materials))
@variable(model,
prod[p=products] ≥ min_prod[products_index[p]],
Int
)
@expression(model,
total_used_material[m=materials],
sum(
material_per_product[products_index[p], materials_index[m]] * prod[p]
for p in products
)
)
# total_mat_cost = sum(
# total_used_material[m] * material_cost[m]
# for m, _ in enumerate(materials)
# )
total_mat_cost = sum(total_used_material .* material_cost)
# total_mat_cost = dot(total_used_material, material_cost)
revenue = sum(prod .* selling_price)
profit = revenue - total_mat_cost
time_expenditure = sum(hours_to_assemble .* prod)
@objective(model, Max, profit)
@constraint(model, time_expenditure ≤ time_availability)
optimize!(model)
return [value(prod[p]) for p in products], objective_value(model), model
end
Results
Running this code for different time availabilities, we get the following plots:
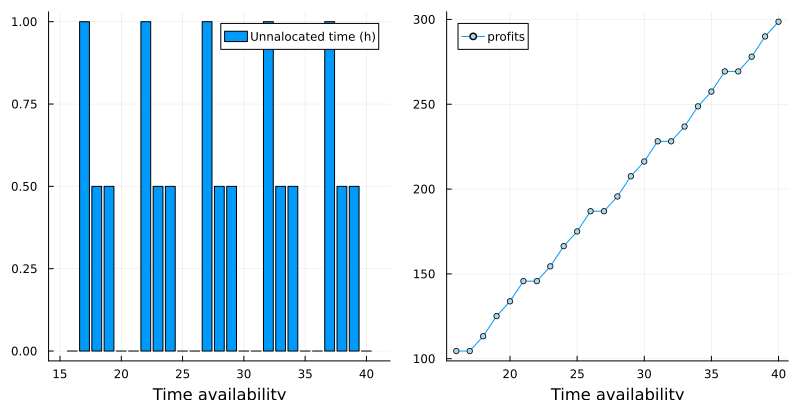
The actual values only make sense within the context of the prices, so I won’t show them here. What is interesting, though, is that you can see the nonlinearity of the profit with respect to time availability. If you only worked with linear programming before, it is often surprising how “simply” forcing the variables to be integer lead to such cases.
